Home Resources for Co-Design Programs For-loops-auto-vec For-loops-auto-vec_poor-auto-vec

For loops poor auto-vectorization

Based on metrics provided by Extrae (version 3.8.3) and displayed by Paraver (version 4.9.0), we are going to explore how we can detect and analyze if a program is using vectorization in an inefficient way.

Setup for this experiment:

Vector addition kernel: Arrays of size 134 million elements;
Matrix multiplication kernel: Square matrices of 2048 by 2048 elements;

Performance metrics for this experiment (*):

AVL - Average Vector Length: This metric represents the ration between the number of double-precision floating-point operations and the number of double-precision floating-point vector instructions.
OPC - Operations per cycle: This metric describes the ratio between the number of double-precision floating-point operations and the total number of useful cycles.

The first step is to examine the verbose provided by the compiler. To know more about this topic, we refer the reader the reader to the For loops poor auto-vectorization version.

The second step is to analyze the suitable performance metrics, which in this scenario is going to be the AVL and OPC, for each of the examples.

Vector Addition

Compiler report:

Begin optimization report for: vadd(double *, double *, double *, int)

    Report from: Loop nest & Vector optimizations [loop, vec]

LOOP BEGIN at vadd.c(4,2)
<Peeled loop for vectorization, Multiversioned v1>
   remark #15389: vectorization support: reference c[i] has unaligned access   [ vadd.c(4,25) ]
   remark #15389: vectorization support: reference a[i] has unaligned access   [ vadd.c(4,30) ]
   remark #15389: vectorization support: reference b[i] has unaligned access   [ vadd.c(4,35) ]
   remark #15381: vectorization support: unaligned access used inside loop body
   remark #15305: vectorization support: vector length 8
   remark #15309: vectorization support: normalized vectorization overhead 0.840
   remark #15301: PEEL LOOP WAS VECTORIZED
LOOP END

LOOP BEGIN at vadd.c(4,2)
<Multiversioned v1>
   remark #25228: Loop multiversioned for Data Dependence
   remark #15389: vectorization support: reference c[i] has unaligned access   [ vadd.c(4,25) ]
   remark #15389: vectorization support: reference a[i] has unaligned access   [ vadd.c(4,30) ]
   remark #15389: vectorization support: reference b[i] has unaligned access   [ vadd.c(4,35) ]
   remark #15381: vectorization support: unaligned access used inside loop body
   remark #15305: vectorization support: vector length 8
   remark #15309: vectorization support: normalized vectorization overhead 1.778
   remark #15300: LOOP WAS VECTORIZED
   remark #15442: entire loop may be executed in remainder
   remark #15450: unmasked unaligned unit stride loads: 2
   remark #15451: unmasked unaligned unit stride stores: 1
   remark #15475: --- begin vector cost summary ---
   remark #15476: scalar cost: 8
   remark #15477: vector cost: 1.120
   remark #15478: estimated potential speedup: 6.380
   remark #15488: --- end vector cost summary ---
LOOP END

LOOP BEGIN at vadd.c(4,2)
<Remainder loop for vectorization, Multiversioned v1>
   remark #15389: vectorization support: reference c[i] has unaligned access   [ vadd.c(4,25) ]
   remark #15389: vectorization support: reference a[i] has unaligned access   [ vadd.c(4,30) ]
   remark #15389: vectorization support: reference b[i] has unaligned access   [ vadd.c(4,35) ]
   remark #15381: vectorization support: unaligned access used inside loop body
   remark #15305: vectorization support: vector length 8
   remark #15309: vectorization support: normalized vectorization overhead 0.840
   remark #15301: REMAINDER LOOP WAS VECTORIZED
LOOP END

LOOP BEGIN at vadd.c(4,2)
<Multiversioned v2>
   remark #15304: loop was not vectorized: non-vectorizable loop instance from multiversioning
LOOP END

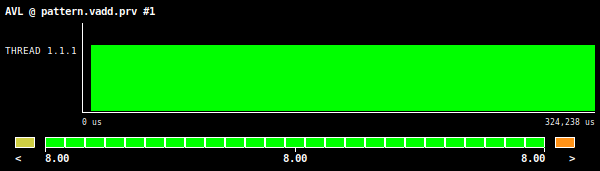for-loops-poor-auto-vec-exp-1-AVL_pattern-vadd Figure 1: Vector addition AVL value, using an array size of 134 million elements.

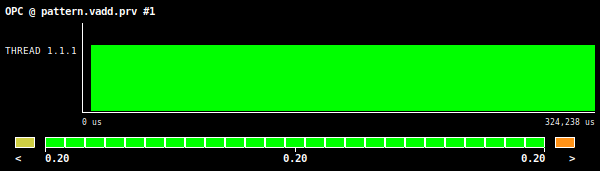for-loops-poor-auto-vec-exp-1-OPC_pattern-vadd Figure 2: Vector addition OPC value, using an array size of 134 million elements.

Even though we are not fully vectorizing the vector addition kernel, the AVL value is equal to the theoretical value of the vector length of the tested hardware architecture (Intel AVX512 ISA). This is due to the fact that, in this example, the peeled and remainder loops do not translate into a heavy performance penalty. Therefore, for simple algorithms, the poor vectorization efficiency should be detected by the information provided by the compiler, otherwise it will be difficult to detect such symptom with this AVL metric. Looking at the OPC metric, we get a low value of 0.2, which again, given the simplicity and low arithmetic density of the example, does not give us a clear picture regarding the efficiency of the vector instructions and so the user should rely on the information provided by the compiler.

Matrix multiplication

Compiler report:

Begin optimization report for: matmul(const double *, const double *, double *, const int, const int, const int)

    Report from: Loop nest & Vector optimizations [loop, vec]

LOOP BEGIN at /gpfs/home/bsc33/bsc33172/POP/auto-vectorization/for-loops-poor-auto-vec/src/matmul.c(6,2)
   remark #25445: Loop Interchange not done due to: Data Dependencies
   remark #25446: Dependencies found between following statements:  [From_Line# -> (Dependency Type) To_Line#]
   remark #25447: Dependence found between following statements:  [8 -> (Flow) 8]
   remark #25447: Dependence found between following statements:  [8 -> (Anti) 8]
   remark #25451: Advice: Loop Interchange, if possible, might help loopnest. Suggested Permutation : ( 1 2 3 ) --> ( 1 3 2 )
   remark #15541: outer loop was not auto-vectorized: consider using SIMD directive

   LOOP BEGIN at /gpfs/home/bsc33/bsc33172/POP/auto-vectorization/for-loops-poor-auto-vec/src/matmul.c(7,3)
      remark #15541: outer loop was not auto-vectorized: consider using SIMD directive

      LOOP BEGIN at /gpfs/home/bsc33/bsc33172/POP/auto-vectorization/for-loops-poor-auto-vec/src/matmul.c(8,4)
         remark #15344: loop was not vectorized: vector dependence prevents vectorization
         remark #15346: vector dependence: assumed FLOW dependence between C[i*N+j] (8:25) and C[i*N+j] (8:25)
         remark #15346: vector dependence: assumed ANTI dependence between C[i*N+j] (8:25) and C[i*N+j] (8:25)
      LOOP END
   LOOP END
LOOP END
===========================================================================

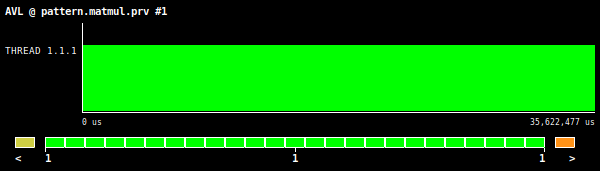for-loops-poor-auto-vec-exp-1-AVL_pattern-matmul Figure 3: Matrix multiplication AVL value, using square matrices of 2048 by 2048 elements.

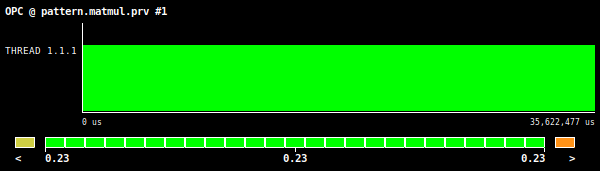for-loops-poor-auto-vec-exp-1-OPC_pattern-matmul Figure 4: Matrix multiplication OPC value, using square matrices of 2048 by 2048 elements.

In this example, the aforementioned metrics (mostly AVL) definitely provide insightful information regarding the efficiency of using vector instructions. For example, if we look at the results given in Figure 3 we see that the AVL value is one. This value is significantly less the theoretical value for the tested hardware architecture (Intel AVX512 ISA) which is 8. The OPC value (Figure 4), also give us a lower value of 0.23 which can be understood as a symptom of poor use of vector instructions, but this metric alone is not sufficient enough to clearly see this issue.

(*) These performance metrics are being developed by MEEP and POP2 projects.