JuKKR-kloop master version analysis

Environment

All measurements have been performed on one node of the CLAIX-2018 cluster of RWTH Aachen University. A single node is a two-socket system featuring Intel Skylake Platinum 8160 CPUs each. One CPU has 24 cores running with a base frequency of 2.1 Ghz. SubNUMAClustering is enabled which means that there are 4 NUMA domains each with 12 cores in total. The OpenMP threads were pinned to CPU cores of one NUMA domain in a close fashion using the following environment variables:

export OMP_PLACES=cores
export OMP_PROC_BIND=close

Scalability

The original implementation of the k-points integration loop shows very poor strong scalability with an increasing number of OpenMP threads as shown in the figure below:

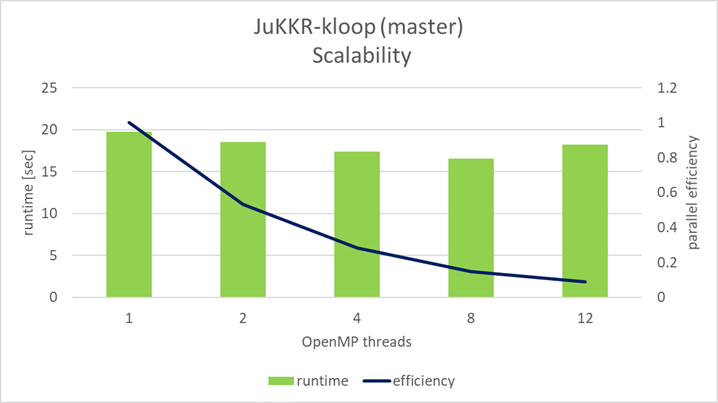
Already when using 2 OpenMP threads only a parallel efficiency of 53% is achieved. Even worse when the NUMA domain is completely filled with threads the parallel efficiency is only 9%.

Efficiencies

We collected additive hybrid POP efficiency metrics which are shown in the table below:

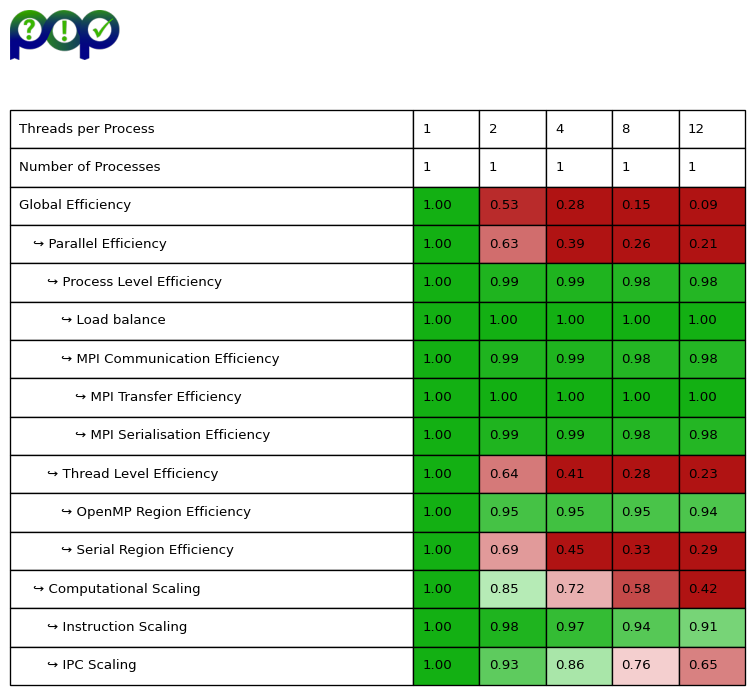
First the Global Efficiency matches with the parallel efficiency from the strong scaling measurements. Furthermore, the POP metrics provide hints on reasons for this poor scalability behavior of the original k-points integration implementation.

Most striking is the huge drop in the Serial Region Efficiency down to only 29% when using 12 OpenMP threads. This shows that a significant part of the code is executed in serial which according to Amdahl’s law limits the scalability. In fact the whole matrix setup for each k-point is done only by the master thread. Only inside the \(\texttt{zgetrf}\) call into the Intel MKL multiple OpenMP threads are forked to collaborate on the LU decomposition of matrix \(M_k\).

Moreover, by looking at the Computational Scaling one can recognize that the IPC Scaling and the Frequency Scaling are both not optimal. The decrease in the Frequency Scaling can be explained by the Intel Turbo Boost technology. If only a single thread is running at all the CPU can easily run with a Turbo Boost frequency of more than 3.0 GHz. However, the more threads are running concurrently on different cores of the CPU the less each individual core can make use of the Turbo Boost feature due to internal power and thermal constraints the CPU needs to meet.

Finally, the decreasing IPC Scaling can probably be explained by False-Sharing effects inside the NUMA domain. Recall that for each k-point the matrix \(M_k\) is setup in serial by the master thread. Also each matrix has a size of \(32 \times 32\) complex number data elements. This means a single matrix requires only around 16 kB of memory which easily fits into the L1-cache of current systems. In our case the L1-cache has a capacity of 32 kB. So most likely the matrix will reside in the L1-cache after being setup. If now multiple threads access the matrix when collaboratively computing an LU decomposition data elements on the same cache line are probably accessed by different threads running on different CPU cores which causes False-Sharing. This results in additional data transfers between the CPU caches. So each CPU has to perform additional cycles to wait on these data transfers which decreases the IPC the more threads are involved.