Indirect reductions with atomic or critical constructs on large data structures

A pattern that appears on many codes computing on a grid of topologically connected nodes is the reduction of values on the nodes with possible multiple contributions from neighboring nodes. This pattern typically results in codes with reduction operations through indirection on a large array that use atomic or critical constructs to avoid the potential data race when updating it.

This pattern occurs in finite element codes (such as Alya), n-body codes, or in graph processing codes when mutual exclusion is needed when accessing neighbors (such as SPECFEM3D).

The parallelization of this pattern consists traditionally of loop parallelism using OpenMP, for example using the taskloop construct, as depicted in the next code snippet:

#pragma omp parallel masked
#pragma omp taskloop
for (i = 0; i<SIZE; i++) {
   NN = n_neighs[i];
   for (int n=0; n<NN; n++) {
      type_t contribution =  f(current_state, i, n);
      #pragma omp atomic //or critical
      next_state[get_index(i,n)] += contribution;
   }
}

The array next_state is accessed (and updated) concurrently by multiple threads via an array of indexes: different iterations will be updating different positions of the array and there is the potential for races, so the code must include the appropriate synchronization mechanisms such as the atomic construct depicted in the code.

So this pattern consists of enclosing the update operation in an atomic or critical OpenMP construct so we can ensure that races on the updates are avoided.

This approach has two potential issues:

• First is the overhead of how the atomicity is implemented by the compiler and runtime. Even if the accesses are very scattered and there are no actual conflicts, this overhead can have an important impact if it is comparable in magnitude to the duration of the computation of the contribution. In this regard, the important thing in this solution is the ratio between the granularity of the computation and the part inside the atomic (or critical) block (including the overhead of each option which has been measured as 24 ns and 0.05 ns for critical and atomic respectively in an Intel Xeon E5645 processor). As an example, if this ratio is 5:1, only 5 threads will be able to work in parallel while if this ratio is 1000:1 there is no problem with this option at all.
• The second issue would happen if the indirections pattern results in conflicts, causing a high-contention.

In real practice, if the array is sufficiently large, the first issue may be more important in terms of performance degradation, causing a low IPC value that prevents a good Computation Scalability. An example of these symptoms can be seen in the following images. These results where obtained in Nord III using the alya-asm program:

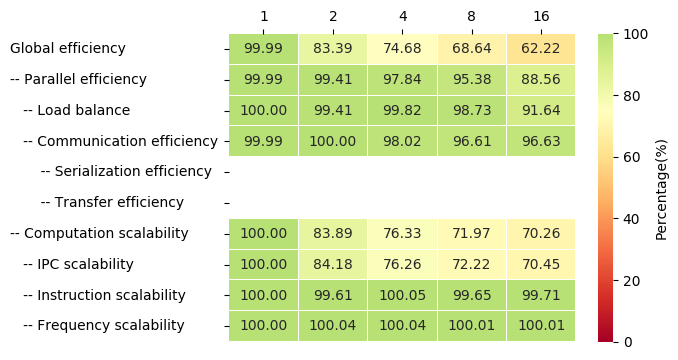
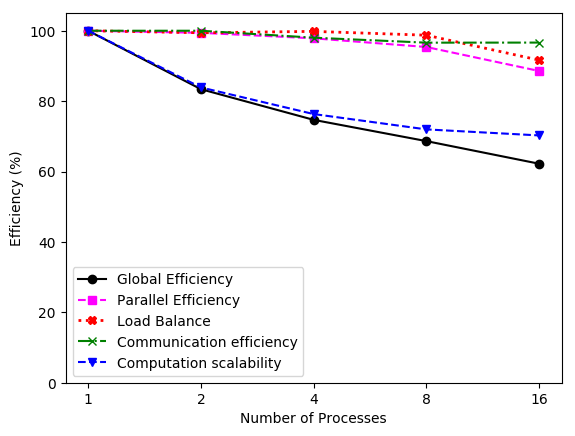
Other strategies have been proposed in the literature to implement this loop parallelism, like coloring or substructuring techniques to circumvent the race condition. The main drawback of the first technique is the IPC decrease due to bad spatial locality. The second technique avoids this issue but requires extensive changes in the implementation. An alternative, based on task parallelism, is to use multidependencies, an extension to the OpenMP programming model, that solves both aforementioned problems.