Performance Optimisation and Productivity
Replicating computation to avoid communication (gemm)
Pattern addressed: High weighted communication in between ranks
This pattern can be observed in parallel algorithms where a large fraction of the runtime is spent calculating data on individual processes and then communicating that data between processes. An example of such a parallel algorithm is molecular dynamics, where N particles interact with each other. The equation of motion to be solved is
(more...)
The best-practice presented here can be used in parallel algorithms where a large fraction of the runtime is spent calculating data on individual processes and then communicating that data between processes. For such applications, the performance can be improved by replicating computation across processes to avoid communication. A simple example can be found in molecular dynamics, where we have the computation of the interactions between N particles. The equations of motion to be solved are
where \({\bf F}\) is the vector of the total force, N is the total number of particles and \(\bf {a}_{i,j}\) is the acceleration vector. The calculation needs to be performed for every particle with respect to every other.
With the communication-avoiding approach, the MPI communication overhead scales with the number of MPI processes so, with a large enough number of particles, the computation dominates and significant speed-ups can be achieved.
In Figure 1, the speed-up plots for N=100, N=1,000, N=10,000 and N=100,000 are shown. For N=100 and N=1000 the computational part of the code doesn’t compensate for the MPI communication, so the application doesn’t scale efficiently. Contrary to the Pattern, this effect is highly reduced when more particles are used (i.e. due to having more computation per MPI process). For N=10,000 and N=100,000, in fact, the speed-up of the application is over \(80 \%\) for all node counts.
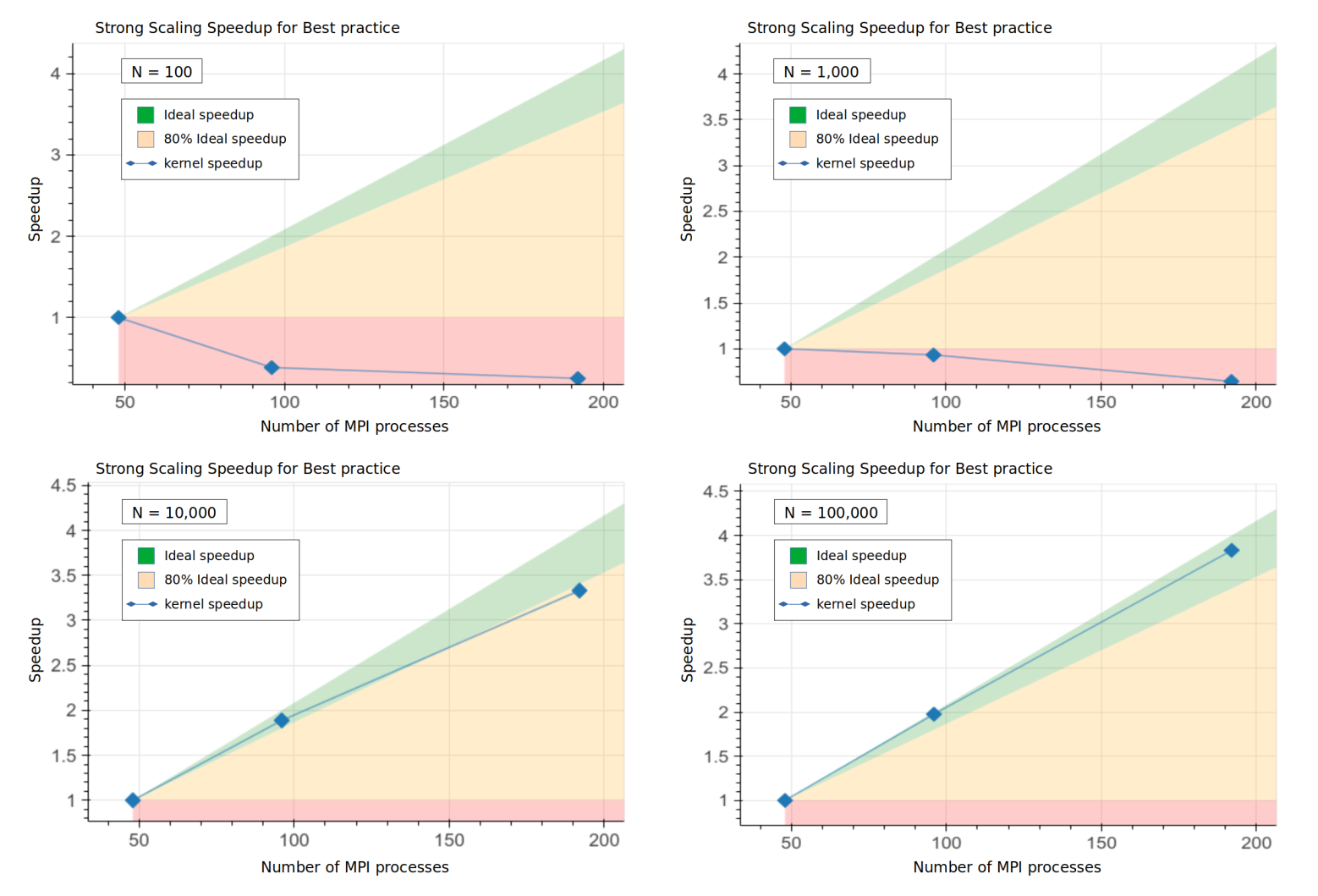Figure 1: Speed-up plot for N=100, N=1,000, N=10,000 and N=100,000. In all four cases the time stepping loop has 10 iterations (NUMSTEPS=10).
Recommended in program(s): High weighted communication in between ranks ·
Implemented in program(s): Replicating computation to avoid communication ·
