
Performance Optimisation and Productivity
High weighted communication in between ranks
Usual symptom(s):- Transfer Efficiency: The Transfer Efficiency (TE) measures inefficiencies due to time in data transfer. (more...)
This pattern can be observed in parallel algorithms where a large fraction of the runtime is spent calculating data on individual processes and then communicating that data between processes. An example of such a parallel algorithm is molecular dynamics, where N particles interact with each other. The equation of motion to be solved is
\(\bf {F}\) is the vector of the total force, N is the total number of particles, \(\bf {a}_{i,j}\) is the acceleration vector and it has to be computed for every particle w.r.t. every other.
A frequently used approach is to use the Atom Decomposition algorithm [1], where the force computation is split among different processes:
for process = 1, M {
1. compute partial forces for particles assigned to this process
2. send particle forces needed by other processes and receive particle forces needed by this process
3. update position and velocity for particles assigned to this process
}
where M is the total number of MPI processes. In this way, when the number of particles is large the communication due to MPI calls becomes a significant bottleneck, given that the number of MPI calls (point 2.) scales quadratically with the number of particles.
In Figure 1, the speed-up plot is shown for both cases. The larger the number of nodes, the more important the MPI overhead. This effect depends on the number of particles as well, the larger case shows a more severe slow down with respect to the smaller case.
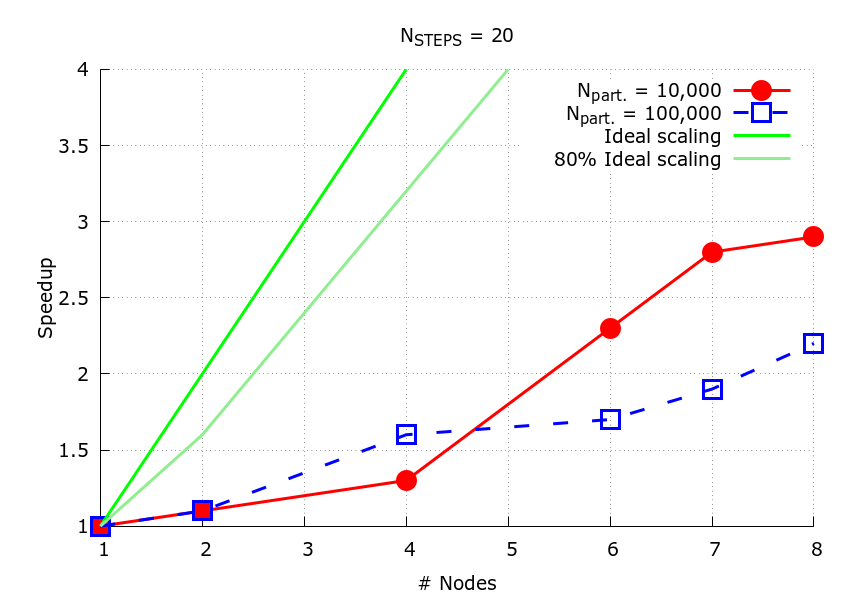 Figure 1: Speedup plot. The larger (
Figure 1: Speedup plot. The larger (N=100,000) and smaller cases (N=10,000) are shown in blue and red, respectively. The dark-green continuous line represents the ideal scaling, while the light-green continuous line represents the 80% ideal scaling.
In Table 1, the Global, Transfer and Serialisation efficiencies are shown for the N=10,000 particles case for 1, 2 and 4 nodes. In all cases, the MPI transfer efficiency is very low while the Serialisation efficiency is quite high but it slowly decreases with increasing number of nodes. The overall effect is a drastic reduction of the performance and very poor Global efficiency.
| Number of Processes | 48 | 96 | 192 |
|---|---|---|---|
| Global Efficiency | 0.05 | 0.05 | 0.06 |
| MPI Transfer Efficiency | 0.12 | 0.13 | 0.16 |
| MPI Serialisation Efficiency | 0.12 | 0.13 | 0.89 |
Table 1: POP metrics for the smaller cases (N=10,000).
[1] Plimpton et al. (1995) [https://doi.org/10.1006/jcph.1995.1039]
Recommended best-practice(s): Related program(s):