Low computational performance calling BLAS routines (gemm)

In many scientific applications, parallel matrix-matrix multiplications represent the computational bottleneck. Consider the following matrix-matrix multiplication:

where, \(\bf {A}\) is a matrix with \(N_m\) rows and \(N_k\) columns (i.e. \(N_m \times N_k\)), \(\bf {B}\) is a \(N_k \times N_n\) matrix so that \(\bf {C}\) is a \(N_m \times N_n\) matrix.

In the case where each process has access to \(\bf {A}\) and \(\bf {B}\), a strategy to parallelize the work is to divide \(\bf{B}\) into blocks so as to partition the computation over all the processes, and use the BLAS dgemm routine on the individual blocks. A sketch of the aforementioned strategy can be represented as follows, where for simplicity we assume the number of columns splits evenly over the processes:

where \(\bf {C}_b\) and \(\bf{B}_b\) are matrix blocks generated by splitting over the columns. For \(p\) processes, the blocks \(\bf {B}_b\) are \(N_k \times N_w\), where \(N_w=N_n/p\), and the blocks \(\bf{C}_b\) are \(N_m \times N_w\). In this way, the higher the number of processes \(p\), the smaller the number of columns of \(\bf{B}_b\) and \(\bf{C}_b\). The pseudo-code implementation of the aforementioned algorithm can be:

  given:
   N_m, N_n, N_k

  execute:
   get_my_process_id(proc_id)
   get_number_of_processes(n_proc)

   DEFINE first, last, len_n_part AS INTEGER
   DEFINE alpha, beta AS DOUBLE

   first = float(N_n) * proc_id / n_proc
   last = (float(N_n) * (proc_id + 1) / n_proc) - 1

   len_n_part = last - first + 1;

   SET alpha TO 1.0
   SET beta TO 0.0
   call dgemm('N','N',N_m, len_n_part, N_k,alpha ,A, N_m, B[:,first:last], N_k, beta ,C, N_m)

In an ideal case, when the number of processes is doubled, the computational time halves. This strategy has been used in software implementing density functional theory (DFT). However, a POP Audit (see related report bellow) for one such application showed a low global efficiency and a non-optimal performance. One of the sources for the lack of performance was the poor Computation Scaling due to the aforementioned splitting of the matrix-matrix multiplications.

Further work undertaken by POP in a ‘Proof of Concept’ study identified that certain splitting of one (or both) input matrices can result in non-optimal performance. The best-practice page is intended to show the importance of undertaking experiments to identify optimal matrix splittings to ensure good computational performance.

Speedup tests

A simple benchmark code is used to measure the parallel scaling for the pattern, by replicating the amount of computation for \(\bf{A} \times \bf{B}_b\) for processes on a single compute node. For timing purposes there is no need to run the actual computation on all compute nodes, since the computation per node is identical.The three matrices have size \(N_n \times N_n\) where \(N_n = 3600\).

The scaling plot below was obtained using the sequential dgemm subroutine from MKL in the pattern described above. For block multiplication dgemm parameters \(alpha\) and \(beta\) are set to \(1.0\) and \(0.0\), respectively.

The data below is for a fully loaded compute node on MareNostrum-4 (48 processes), the timing is measured for each process and computation is repeated \(100 \times\) to give measurable timings.

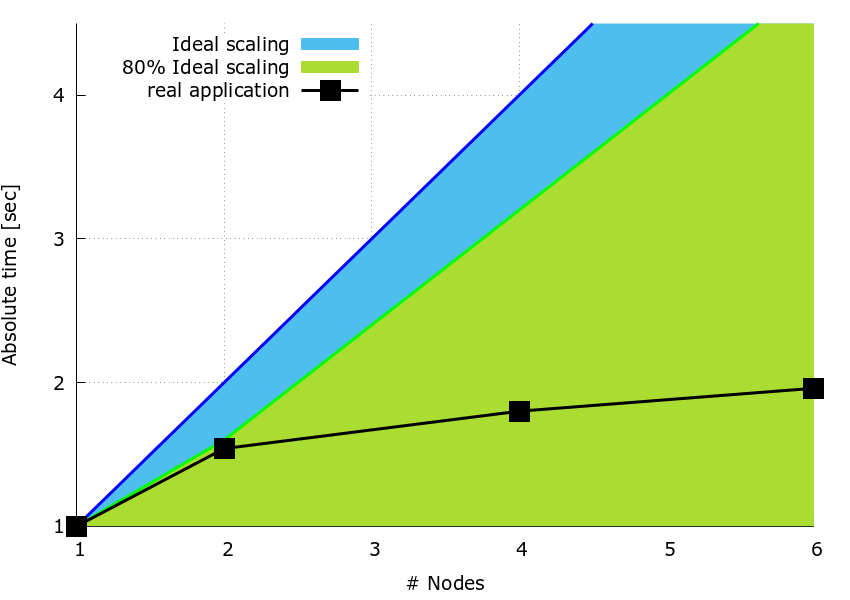Figure 1: speedup plot.

It can be observed that partitioning the work by slitting matrix \(\bf{B}\) over the columns results in a reduced speedup as the number of nodes increases.