Sequence of fine grain parallel loops

This pattern applies to parallel programming models based on a shared memory environment and the fork-join execution model (e.g., OpenMP). The execution of this kind of applications is initialy sequential (i.e., only one thread starts the execution of the whole program), and just when arriving at the region of the code containing potential parallelism, a new parallel region is created and multiple threads will start the execution of the associated code. Parallel execution usually will distribute the code among participating threads by means of work-sharing directives (e.g., a loop directive will distribute the loop iteration space among all threads participating in that region).

There are situations in which this type of parallel applications implements a series of consecutive fine-grained parallel regions. Either because the application performs an iterative process and the parallelization is included within the loop step (code A). Either because the application implements a sequence of parallel loops that are parallelized individually (code B). Finally, Code C shows a typical simulation structure: on the upper most level there is a loop over discrete time steps; then the next level is a loop over discrete spatial elements like particles, atoms, or mesh elements. For each spatial element several computational kernels have to be performed that might depend on each other. Often times the individual computation kernels consist of common operations that are provided by optimized software libraries e.g. Intel’s Math Kernel Library (MKL).

The following snipped illustrates these three scenarios:

void code_A (double *A, int size, int n)
{

   for (int it=0; i<iters; iters++) {
      #pragma omp parallel for
      for (int i=0; i<size; i++) {
         A[i] += f();
      }
   }
}

void code_B (double *A, int size)
{
   #pragma omp parallel for
   for (int i=0; i<size; i++) {
      A[i] += f();
   }

   S();

   #pragma omp parallel for
   for (int i=0; i<size; i++) {
      A[i] += g();
   }

   S();

   #pragma omp parallel for
   for (int i=0; i<size; i++) {
      A[i] += h();
   }
}

void code_C()
{
    for (int t=0; t<MAX_TIME; t+= deltaT) {
        for (int i=0; i<MAX_ELEMS; i++) {
            BLAS_kernel_A(i); // it can be either sequential or parallel
        }

        for (int i=0; i<MAX_ELEMS; i++) {
            BLAS_kernel_B(i); // it can be either sequential or parallel
        }

        for (int i=0; i<MAX_ELEMS; i++) {
            BLAS_kernel_C(i); // it can be either sequential or parallel
        }
    }
}

Both, the opening (fork) and the closing (join) phases of a parallel region have an associated overhead cost that it is accumulated in a repeated succession of small regions causing a higher time penalty than actually required. In addition, if work distribution is not perfectly balance, and the following code has not dependence with the loop computation, there is no way to avoid the parallel barrier execution.

The following trace shows two different effects when executing Code B. First, the overhead introduced by a sequence of fine grain parallel regions. Second, how all the threads are forced to wait on the implicit parallel barrier, and causing a serialization effect (highlighted by the micro-imbalances). Code A will show an equivalent behaviour.

In Code C there are some problems with this kind of parallelization:

1) if BLAS_kernel_B executes a parallel version of the algorithm and its complexity is too low, then the loop over all discrete spatial elements i will result in a sequence of fine grain parallel loops. 2) if there exist no parallel version for BLAS_kernel_A and BLAS_kernel_C, then the scalability of the application is limited by the fraction of the serial runtime of both kernels compared to the total runtime of the application. 3) if parallel versions for BLAS_kernel_A and BLAS_kernel_C exist, then the application may be fully parallelized but an even larger sequence of fine grain parallel loops is created.

In all cases the parallelization is sub-optimal because the parallelization is not applied at the upper most possible level.

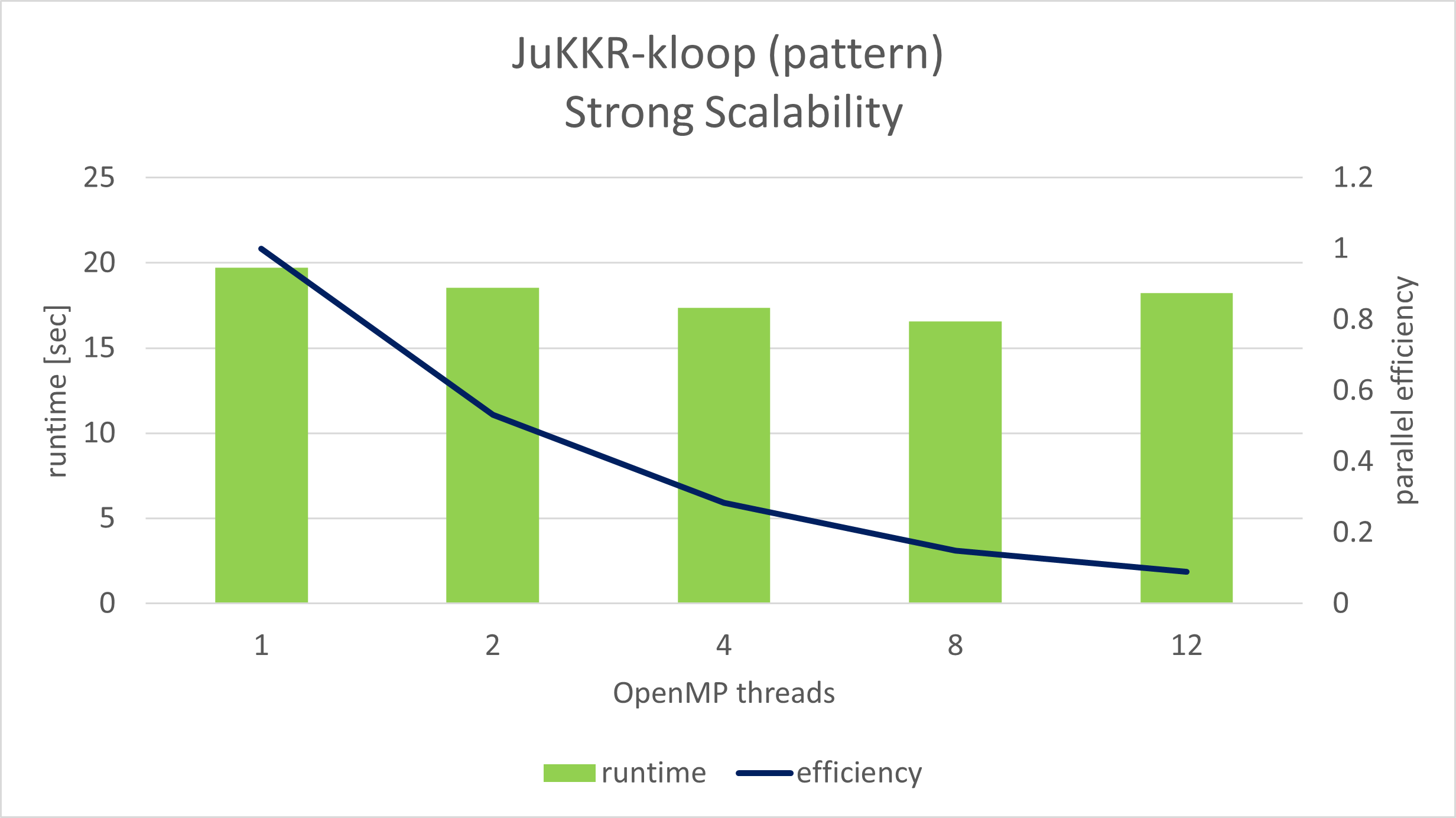
The pattern has been found in the Juelich KKR code family (JuKKR). One important part of the code is a “k-point integration loop”. In this part the code performs a sequence of parallel BLAS kernel calls that produce the effect described in this pattern (code C). The figure above shows a strong scaling experiment of a miniapp extracted from the JuKKR code and focussing on the k-point loop. Up to 8 OpenMP threads the code scales very poorly due to problem 1). BLAS_kernel_A and BLAS_kernel_C are not parallelized and limit the scalability. With 12 threads the scalability gets even worse because now problem 2) becomes visible. The complexity of BLAS_kernel_B is too low such that the overhead induced by the sequence of fine grain parallel loops is now a limiting factor.

In addition this kind of pattern can also be observed in the official OpenMP LULESH benchmark version, where multiple consecutive parallel regions are executed one after the other with usually very small granularity.